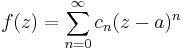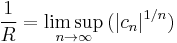Cauchy–Hadamard theorem
In mathematics, the Cauchy–Hadamard theorem is a result in complex analysis named after the French mathematicians Augustin Louis Cauchy and Jacques Hadamard, describing the radius of convergence of a power series. It was published in 1821 by Cauchy,[1] but remained relatively unknown until Hadamard rediscovered it.[2] Hadamard's first publication of this result was in 1888;[3] he also included it as part of his 1892 Ph.D. thesis.[4]
Contents |
Theory for one complex variable
Statement of the theorem
Consider the formal power series in one complex variable z of the form
where 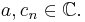
Then the radius of convergence of ƒ at the point a is given by
where lim sup denotes the limit superior, the limit as n approaches infinity of the supremum of the sequence values after the nth position. If the sequence values are unbounded so that the lim sup is ∞, then the power series does not converge near a, while if the lim sup is 0 then the radius of convergence is ∞, meaning that the series converges on the entire plane.
Proof of the theorem
[5] Without loss of generality assume that 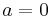 . We will show first that the power series
. We will show first that the power series 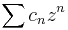 converges for
converges for 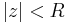 , and then that it diverges for
, and then that it diverges for 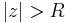 .
.
First suppose 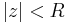 . Let
. Let 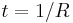 not be zero or ±infinity. For any
not be zero or ±infinity. For any 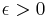 , there exists only a finite number of
, there exists only a finite number of  such that
such that
![\sqrt[n]{|c_n|}\geq t%2B\epsilon](/2012-wikipedia_en_all_nopic_01_2012/I/2a4f0c7540252ea99cea97db82c3727d.png) . Now
. Now 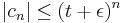 for all but a finite number of
for all but a finite number of 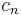 , so the series
, so the series 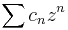 converges if
converges if 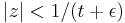 . This proves the first part.
. This proves the first part.
Conversely, for 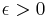 ,
, 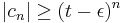 for infinitely many
for infinitely many 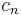 , so if
, so if 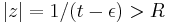 , we see that the series cannot converge because its nth term does not tend to 0.
, we see that the series cannot converge because its nth term does not tend to 0.
The case where t is zero or ±infinity is left for the reader.
Several complex variables
Statement of the theorem
Let  be a multi-index (a n-tuple of integers) with
be a multi-index (a n-tuple of integers) with 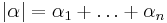 , then
, then  converges with radius of convergence
converges with radius of convergence  (which is also a multi-index) if and only if
(which is also a multi-index) if and only if
![\lim_{|\alpha|\to\infty} \sqrt[|\alpha|]{|c_\alpha|\rho^\alpha}=1](/2012-wikipedia_en_all_nopic_01_2012/I/ed702585e530355633cad55cec4bcf03.png)
to the multidimensional power series
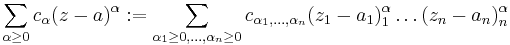
Proof of the theorem
The proof can be found in the book Introduction to Complex Analysis Part II functions in several Variables by B.V.Shabat
Notes
- ^ Cauchy, A. L. (1821), Analyse algébrique.
- ^ Bottazzini, Umberto (1986), The Higher Calculus: A History of Real and Complex Analysis from Euler to Weierstrass, Springer-Verlag, pp. 116–117, ISBN 9780387963020. Translated from the Italian by Warren Van Egmond.
- ^ Hadamard, J., "Sur le rayon de convergence des séries ordonnées suivant les puissances d'une variable", C. R. Acad. Sci. Paris 106: 259–262.
- ^ Hadamard, J. (1892), "Essai sur l'étude des fonctions données par leur développement de Taylor", Journal de Mathématiques pures et appliquées, 4e Série VIII, http://www.archive.org/details/essaisurltuded00hadauoft. Also in Thèses présentées à la faculté des sciences de Paris pour obtenir le grade de docteur ès sciences mathématiques, Paris: Gauthier-Villars et fils, 1892.
- ^ Lang, Serge (2002), Complex Analysis: Fourth Edition, Springer, pp. 55–56, ISBN 0387985921Graduate Texts in Mathematics